Flexagon Fever

This is an article about flexagons. What is a flexagon, you ask? At first glance it looks innocuous enough, like a folded hexagon or square, a child's fortune teller or cootie catcher, or a piece of origami. But look closely and you'll see hidden layers lurking between the front and back. When you fold or pinch corners together, the flexagon "flexes," meaning a formerly hidden layer will come to light as the top layer folds underneath. It all sounds complicated but is really pretty simple when you see an actual flexagon in action. Barring that, a simulation, such as this one created by David King, can help.

Mathematicians refer to flexagons as "mathematical oddities." That's because flexagons have very complex mathematical structures. As the flexagon is flexed, sections shift position to create an almost kaleidoscopic effect, and different faces come into view, in cyclic order. Mathematicians enjoy analyzing the structure and dynamic behavior of flexagons. Laypeople just enjoy playing with them.

This article is about flexagons and the people who love them. It’s about how flexagons can chew you up, spit you out, and leave you wondering where the hours sped to. It’s about how there needs to be a 12-step program for flexaholics. Or perhaps a flexorcist who comes into your home and casts them out.

I flexed my first flexagon at the age of four. My sister Martha had read an article about them, and she and my other sister Ann began making and decorating hexahexaflexagons (so called because they have six sides and six alternating faces). I remember flexing and flexing that flexagon, watching the various faces emerge and disappear, how some appeared far more frequently than others, leaving me flexing like mad to find the hidden faces. I was probably wearing my official Alice in Wonderland blue dress and black patent leather pumps. It would have been lost on me at the time how coincidental it was that I was fascinated with both Alice and flexagons because the man who introduced flexagons to my sisters and the world at large, Martin Gardner in his mathematics columns for Scientific American, is also the author of The Annotated Alice.

Flexagons faded into the background for me after that. It was just this year that they once again raised their creased, hexagonal little heads. My sister, Ann, had the revelation that a tritetraflexagon she created might be an original. Empowered with the Internet for the first time in her flexahistory, she did a quick search and was rewarded with flexagon sites up the wazoo.

It turns out that flexagons have a fascinating history. They were sort of the Game Boys of their time among some of the greatest minds of the 20th-Century. Even Richard Feynman flexed!

Before you could say dodecahexaflexagon, Ann had sparked the interest of several flexagon experts. There’s Vern, who is dedicated to his own version of the trihexaflexagon. Juergen Koeller, a German teacher who uses flexagons to teach math to his high-school students. Harold V. McIntosh, a Mexican professor who has written papers about flexagons. Jean Pedersen, co-author of Build Your Own Polyhedra. David Mitchell, a designer, magician, paperfolder and author of The Magic of Flexagons. Ann even contacted Martin Gardner and sent him some samples. In other words, she discovered a fanatic following of flexamaniacs.

Ann spent many nights burning the midnight oil as she researched and experimented with flexagons, trying out models she hadn't seen before or trying to invent her own. Alas, just when things looked their rosiest because no one recognized this tritetra, Ann found it had been done before. Not to be outdone, she soon devised an intriguing 12-gon. We are still awaiting word as to whether this is an original or not.

Meanwhile, I had found a comfortable niche amongst the hexahexas. These are the second flexagons to be discovered (after the trihexaflexagon, which has six sides and three alternating faces) and the ones that have been anlayzed in the most detail.

Since I’m not particularly mathematically inclined, I tackled flexagons from a creative standpoint, trying to devise designs that were interesting when viewed from either side of the flexagon. (Keep in mind that this is strictly for recreational purposes; I have no delusions of artistic grandeur!)

Soon I found myself making flexagons whenever I had a spare moment. During a school play, I tore a strip off the programme and made a trihexa. I assembled a flexagon kit, consisting of adding-machine paper, a scissor, tape, and colored pencils.

A radial design viewed from one side of the flexagon...

And from the other by flexing and then flipping flexagon on its horizontal axis.

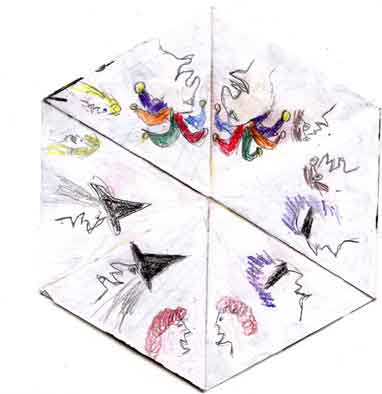
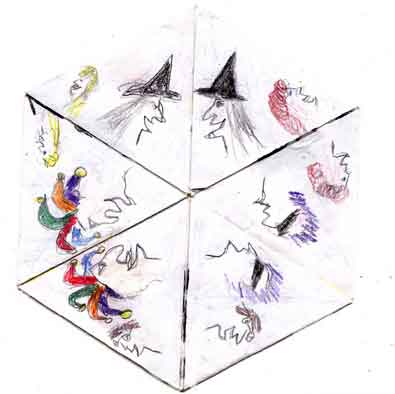
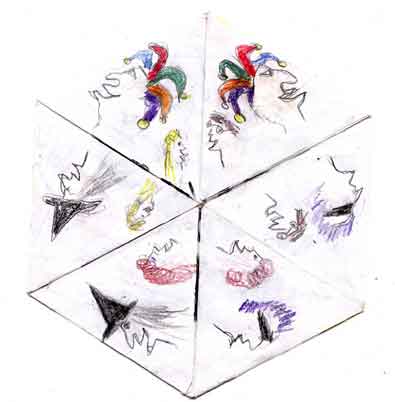
My first designs were radial. Ann told me that radial designs are just fine for the three faces that don't appear as often and only have three degrees of freedom and behave identically to those of the trihexaflexagon. But these designs don't show off the dominant faces of the hexahexa to their best advantage.

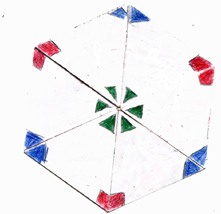
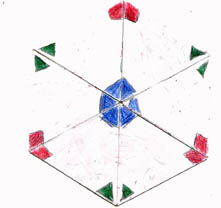
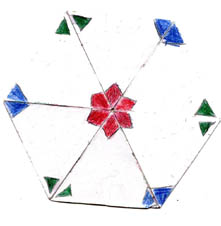
That's because these three dominant faces actually have three variations.

As shown below, you can draw three different designs in the center. Two of the designs will appear on one side of the flexagon; flip it over and start flexing, and you'll see one face again along with another that didn't appear before.

A visual demonstration of how the dominant faces' leaves shift position.

I drew some variations on this three-section theme, but something was amiss. Due to my inability to draw symmetrical objects, I noticed that the drawing that appeared on both sides was reappearing but looked off-kilter.

I became obsessed with solving the hexaflexa mystery. I began carrying flexagons with me in my pocket or purse, just in case I had a spare moment. My family started to get annoyed with me, so I began sneaking in flextime when they weren't around. One day I even came across a secret stash of flexagons stored in a guestroom dresser that I'd forgotten about. I began to not feel whole unless I had a flexagon in my hand.

After much experimentation, I discovered that there are more than three variations. I sent my sister the following e-mail that probably makes little or no sense:

Okay, I figured out the hexaflexagon puzzle. Each of the main faces, 1,2, and 3, has three obvious variations and one sort of hidden variation you won't see if you do symmetrical designs. In two configurations, one set of vertices are in the center, and it is only possible to reach this variation from one side of the flexagon. Either of these, let's call them A1 and B1, can be flexed on any crease. A1 can flex to B1 or B2 (when you flip over the flexagon,of course). B1 can flex to A1 or A2. A2 is a gimpy version, as it can only flex on every other crease.

This side, with the same center vertices, will also appear as a sort of bastardized version on side B, let's call it B2. The center vertices are the same but not in the same order. On A2, if we labeled each consecutive center triangle vertex 1,2, 3... in clockwise direction, if we flip to B2, they will be running counterclockwise. A2 flexes to B1, and B2 flexes to A1.

I'm sure scads of people have figured this out, but I'm kind of pleased that I discovered it just messing on the LIRR and then fiddled and diagrammed until I got it kind of down. Now would someone give me some medication or hit me on the head so I'll stop this already?

Les Pook does a much better job of describing flexagons and their behavior in his book, Flexagons from the Inside Out, (click to read an excerpt).

It turns out that someone did already figure out that one face does appear as a mirror image of itself: Albert Nicholas, professor of education at Monmouth College, Monmouth, IL, in 1957. C'est la vie. I am hoping that he at least did not come up designs that demonstrate this characteristic in such a fascinating way!

To start, let's bring on what I call "The Party":

We start off here: six sets of faces that are all talking to their twins, kind of like a party where everyone first seeks out someone they have something in common with.

Flex again, and now some of the faces have changed position but are still talking to their twins, while the others have buggered off to the rim of the flexagon and are talking to the walls.

Now the faces have changed places, the first set has moved to the rim, while the second set is in the middle—but wait, they're talking to different people!

Now everyone is mingling! What a successful party!

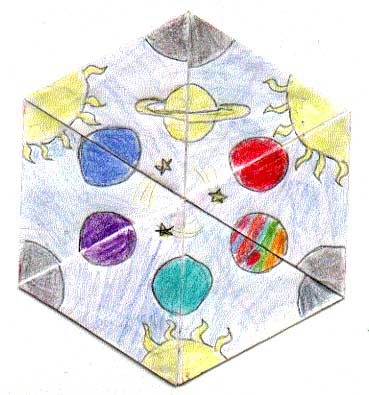
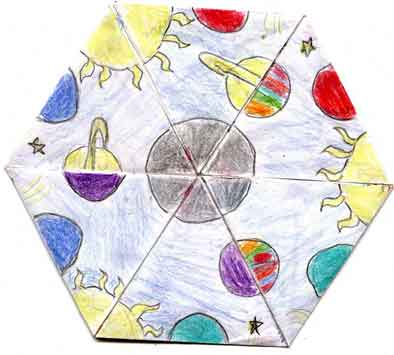
Here are two other fabulous flexagon designs. The first is in an astronomical theme.

Start with a bunch of planets with stars in the center, and a moon and sun on the sides..

On another face, the sun has moved to the center, and there are three intact planets, with six broken planets on the sides.

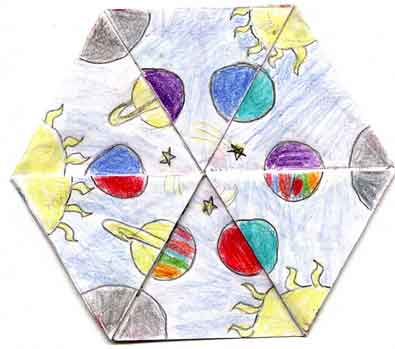
Now the moon is in the center, and the other three planets have moved in, but something has happened to them!

Now the stars are back in the center, but the planets have been halved and patched Boolooroo-like together.

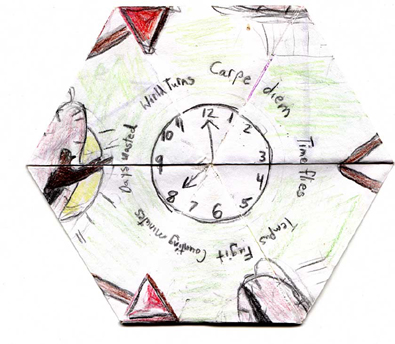
This next design does a better job of showing what is going on. Let's call it bending the space-time continuum. Or maybe just rearranging the clock.

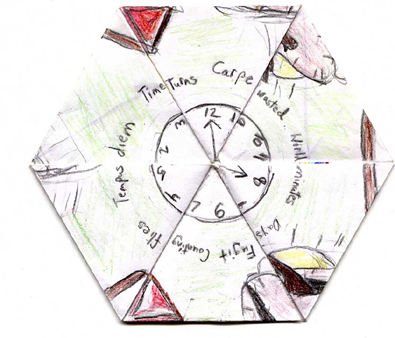
We start with a clock drawn in the center of a 5/1 side of the flexagon with time-related sayings around it.

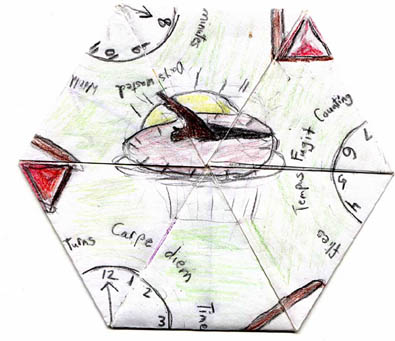On a 4/2 side, we have another time-related theme (that thing in the center is supposed to be a sundial).

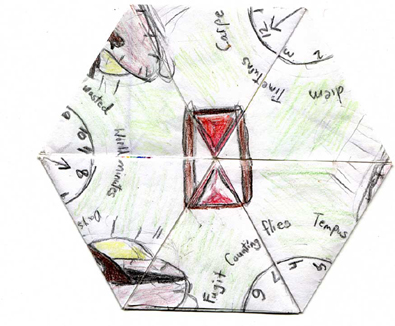
Then we flex to an hourglass.

Flex again and whoa! Looks like Mr. Dali has come to call! The center vertices have rearranged themselves and so have the sayings.

Again, I do not lay claim to having discovered this characteristic. The point is simply the satisfaction of studying an object, finding something out about it, and solving the puzzle.

Ann says she thinks these faces may have six variations, not just four. Hopefully, someone else will figure out whether or not this is true, letting me move on to more useful activities, such as coming up with enough designs for a flexagon exhibit, interactive, of course. Or I'll launch a campaign to get "flexagon" into the dictionary. The possibilities are endless....

—Ela Schwartz

To be continued?