The 8-gon

THE TETRA-OCTA-FLEXAGON

The Flexagon World’s Hidden Gem

Discover for yourself this true cousin of the hexaflexagon!

By Ann Schwartz

Here, from the pages of Build Your Own Polyhedra, by Peter Hilton and Jean Pederson, are directions for making the tetra-octa-flexagon, or 8-gon, as they also call it, together with a very user-friendly analysis.

What is it?

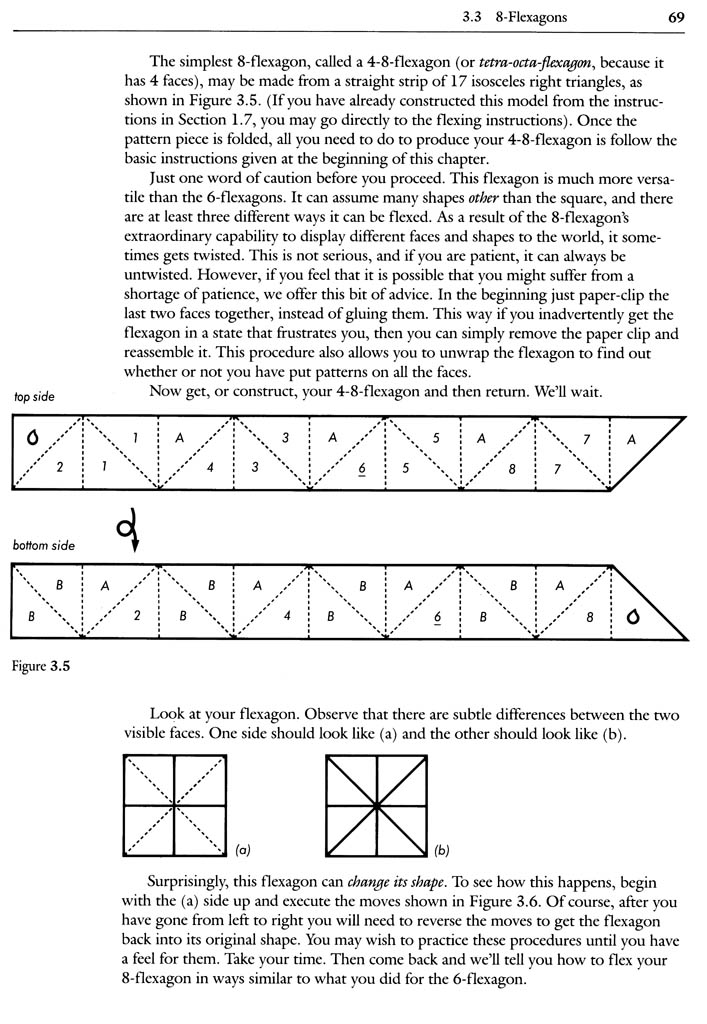
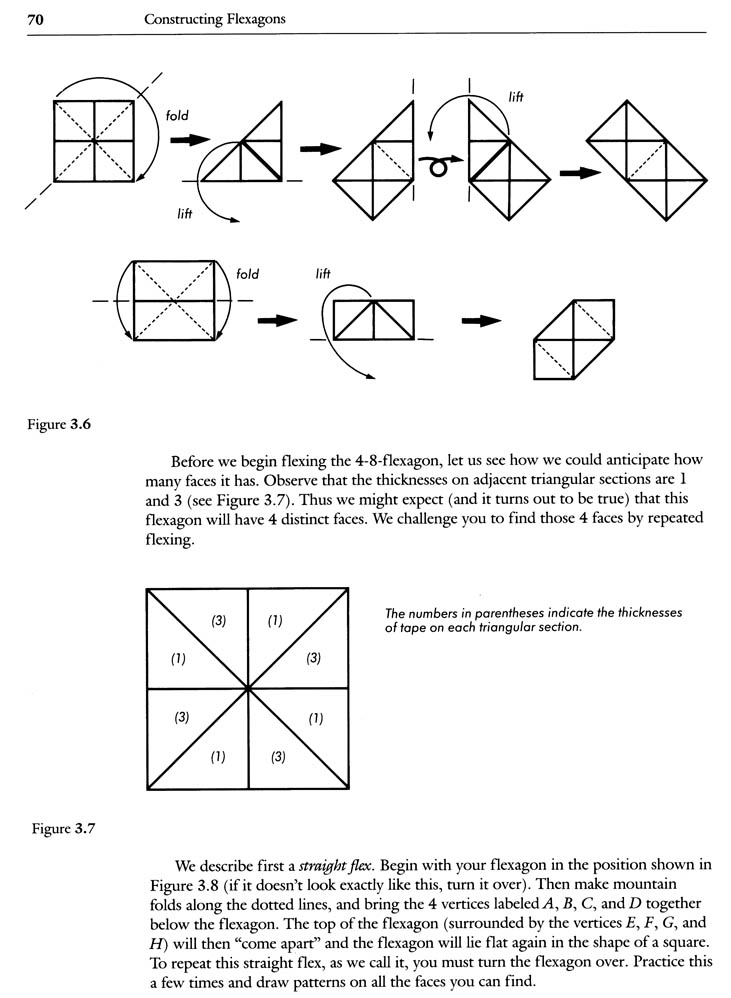
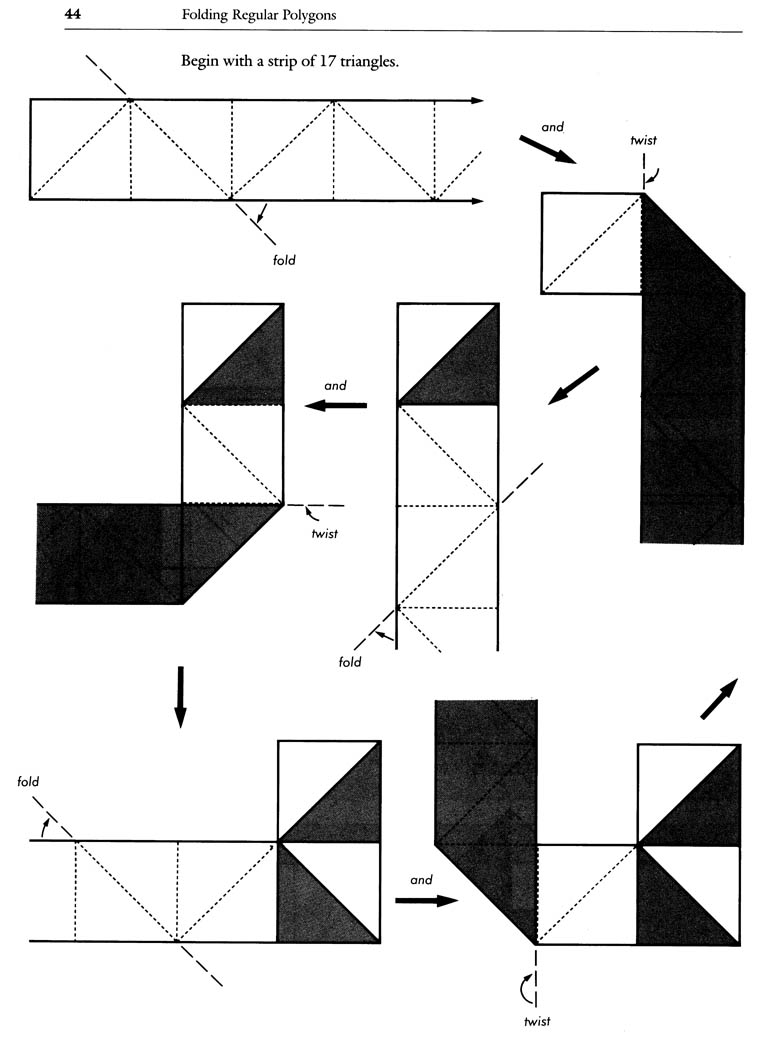
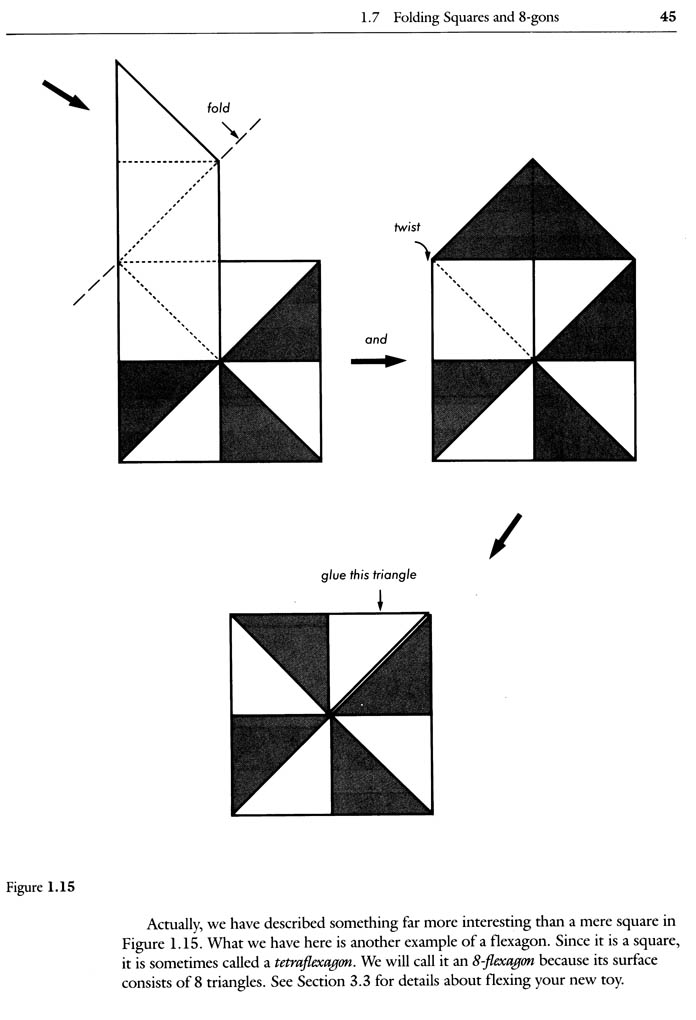
The 8-gon is a square flexagon composed of 8 right triangles, and can be made from a single strip of paper. It can be flexed in the same way a hexaflexagon flexes, and it also can be flexed by using two different types of manipulations that Hilton and Pedersen clearly explain and illustrate in the pages that follow. In addition, as the authors show you, it follows the general laws of flexigation demonstrated by the hexaflexagon—including the capability to have more and more faces when made from longer strips. In these ways the 8-gon is fundamentally different from the tetra-flexagons that have faces composed of squares, not triangles, and which are manipulated with the "book flex." With the 8-gon’s similarities to the hexaflexagon, and its striking differences, I believe that this flexagon pioneers new ground in flexigation, and that understanding its basic principles can give rise to more flexagons made from straight strips.

Why so little known?

I think the reason for this goes back to the original Flexagon Committee and the writings of Martin Gardner. The flexagons explored by Arthur Stone and his associates, the hexaflexagon and the "book fold" tetras, were later promoted through Gardner’s column and books and through them, gained national attention. The 8-gon, according to Hilton and Pedersen, "was discovered independently by many people," probably decades after the Flexagon Committee disbanded. As far as I know, Gardner did not write about it. Without a big national or international platform, the word did not get out.

The 8-gon does turn up in some publications other than Build Your Own Polyhedra. David Mitchell’s The Magic of Flexagons and his booklets on what he calls "silver flexagons," feature the 8-gon made from zig-zag-shaped templates. The zig-zag can also be seen in Anthony Conrad’s flexagon paper and in Les Pook’s Flexagons Inside Out, in the form of net for a three-faced "right angle triangle flexagon." Jean Pedersen herself published an article in Mathematical Digest in 1982 on the 8-gon, six years before the publication of Build Your Own Polyhedra. And Dave Mitchell tells me that it appears in a publication by the British Origami Society.

THE TETRA-OCTA-FLEXAGON REVEALED

From the pages of Build Your Own Polyhedra* by Peter Hilton and Jean Pedersen:

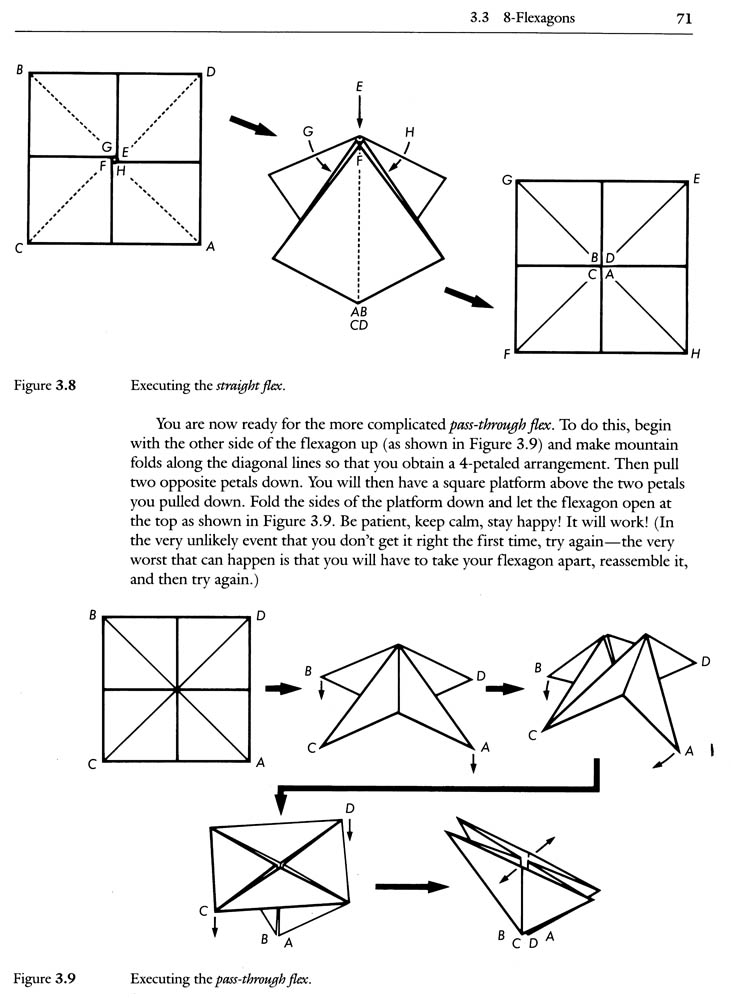
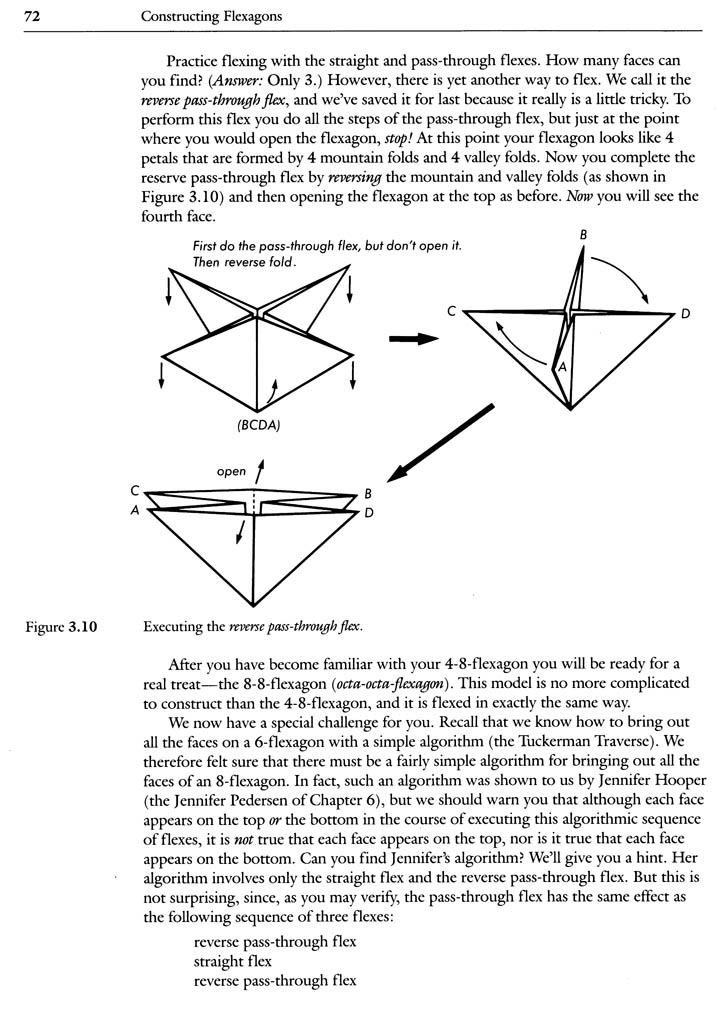
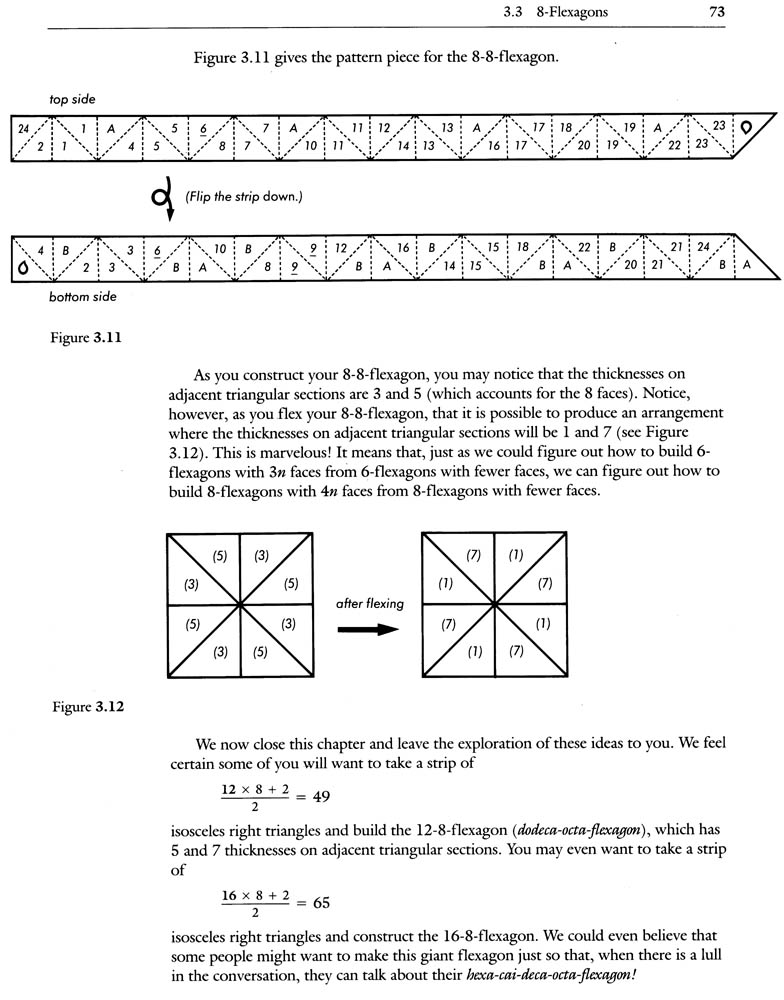
A. 8-Flexagons: The authors present and discuss the 8-gon. This section includes a numbered template for making the 8-gon and illustrations and directions for learning the "pass-through" flex and the "reverse pass-through flex."

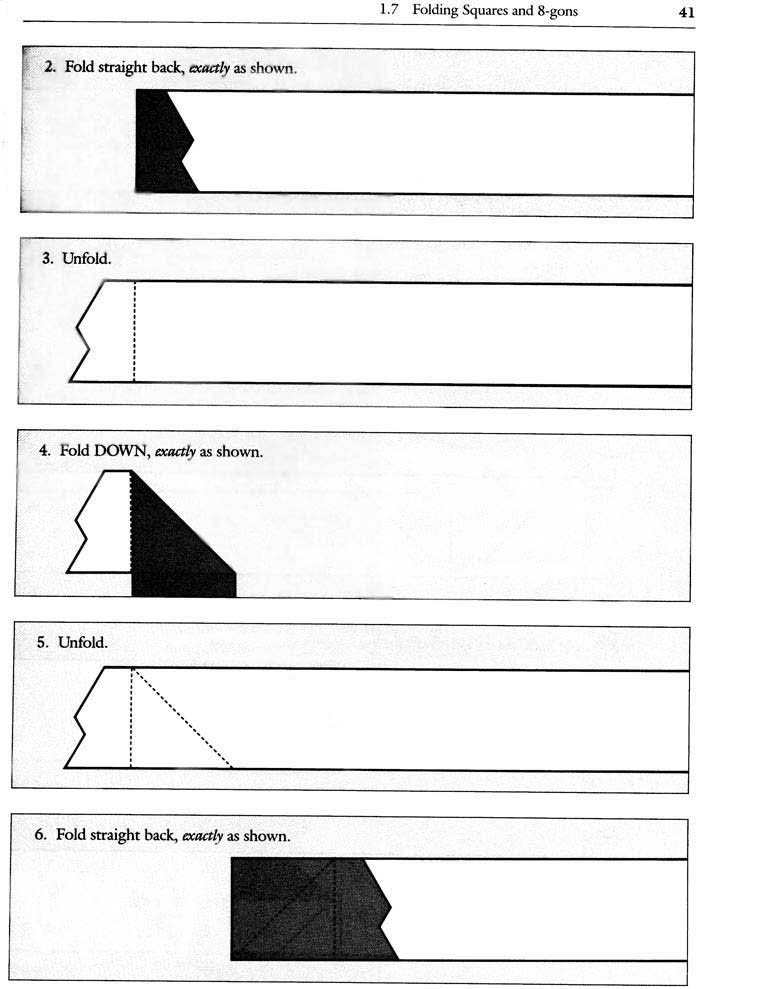
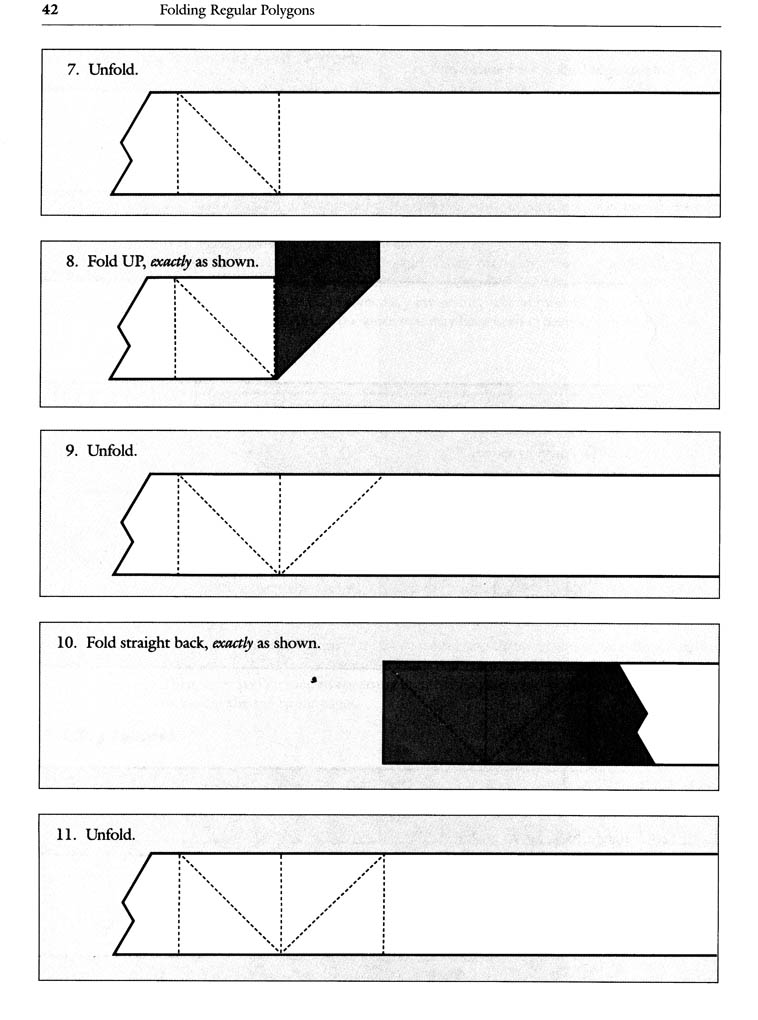
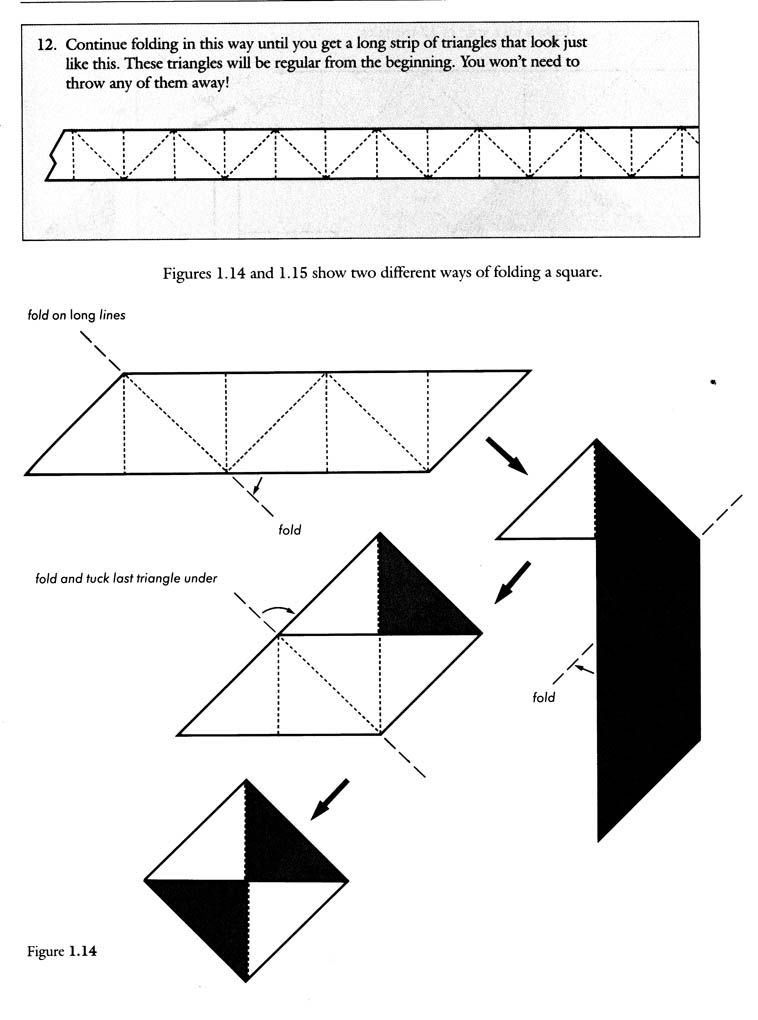
B. Folding Squares and 8-gons: With a series of diagrams, the authors show how to fold squares and 8-gons using a folding pattern from an unnumbered strip.

C. Explanations of how to interpret the illustrations.

Enjoy the 8-gon! And for more information on flexagons, including discussions among flexagon enthusiasts, join the Flexagon Lovers Users Group at http://tech.groups.yahoo.com/group/Flexagon_Lovers/.

A special thank you to Eighthsquare for giving the 8-gon a home, to Jeff Rutzky for his step-by-step scanning instructions and infinite patience, and of course, to Peter Hilton, Jean Pedersen, and Pearson Learning for their permission to reprint parts of Build Your Own Polyhedra (even though Pearson forced us to put annoying copyright lines on the bottom of every page).

*Build Your Own Polyhedra also has instructions for making pop-up solids, rotating rings of tetrahedral, collapsoids, and all sorts of fascinating objects.